插入排序

插入排序是一种从序列左端开始依次对数据进行排序的算法。在排序过程中，左侧的数据 陆续归位，而右侧留下的就是还未被排序的数据。插入排序的思路就是从右侧的未排序区域内取出一个数据，然后将它插入到已排序区域内合适的位置上。

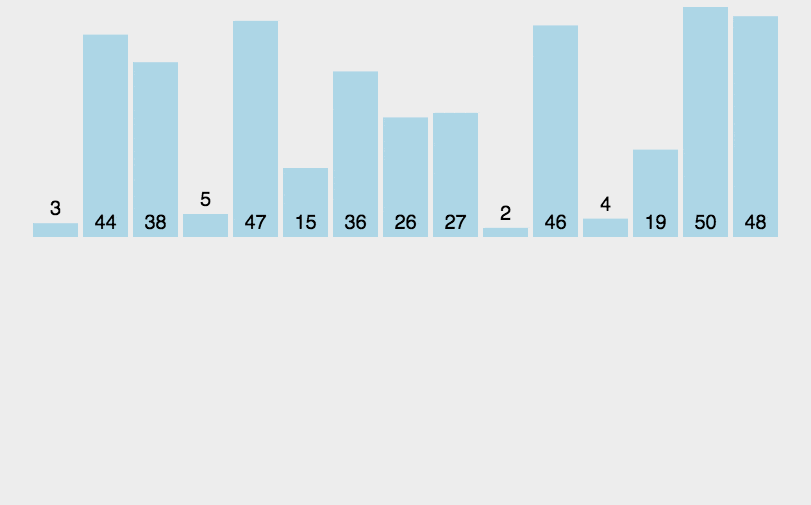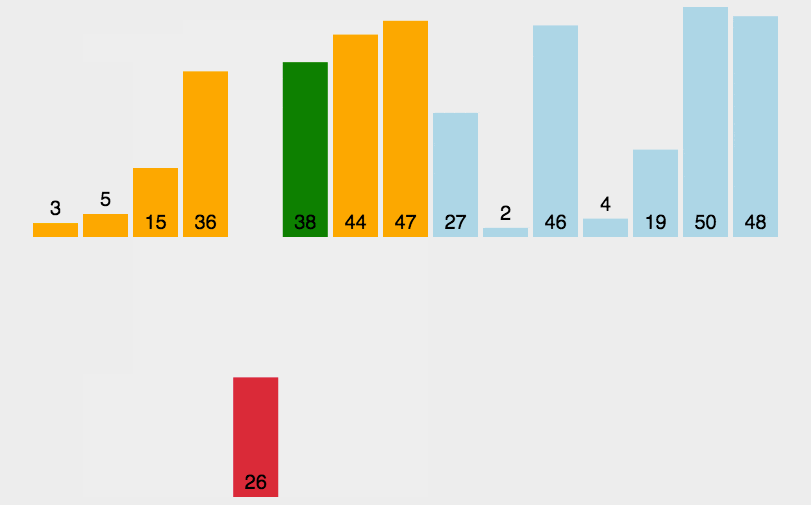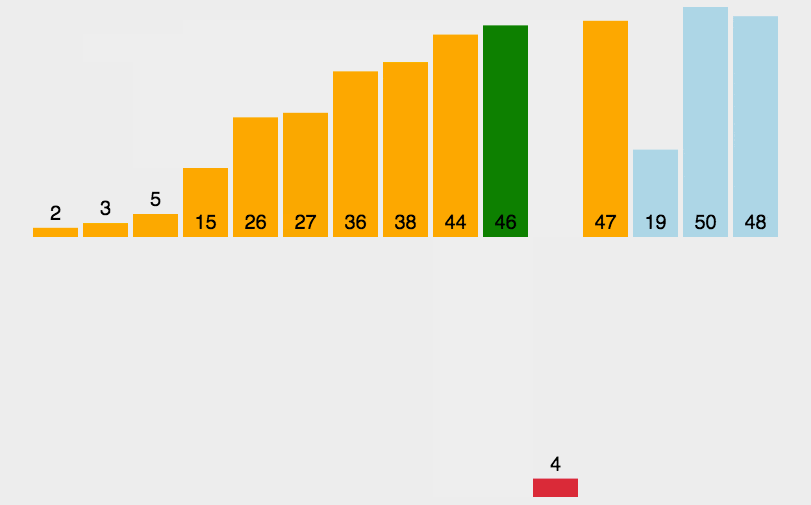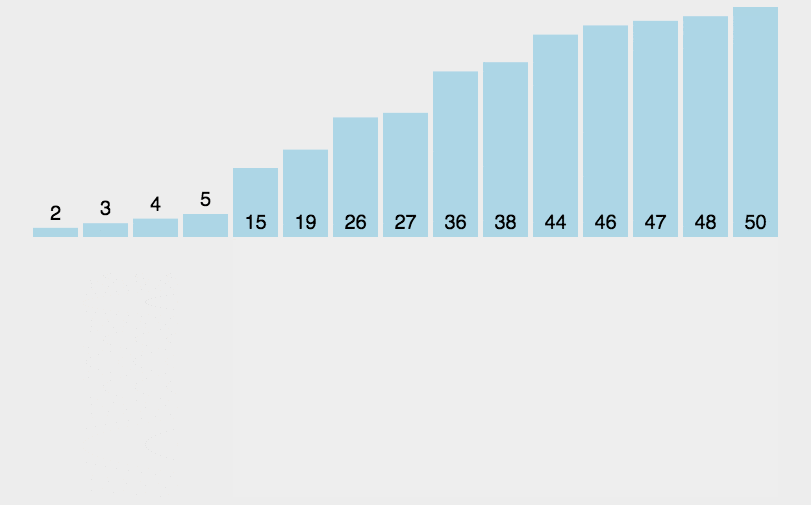
工作原理

• 把一系列数字放在一个未排序的堆里。
• 从堆中挑选一个数字。 你选择哪一个并不重要，但从堆顶挑选是最容易。
• 把这个数插入一个新的数组。
• 从未排序堆中再选择一个数字，并将其插入之前的数组中。 这个数字在第一个数字之前或之后，所以现在这两个数字被排序。
• 再从堆中选择一个数字，并将其插入到数组中的正确排序位置
• 继续这样做，直到堆里没有数字。 最终得到一个空堆和一个排序的数组。

例子

1.对数字 1~9 进行排序

2.首先，我们假设最左边的数字 5 已经完成排序，所以此时只有 5 是已归位的数字。

3.接下来，从待排数字(未排序区域)中取出最左边的数字 3，将它与左边已归位的数字进行比较。若左 边的数字更大，就交换这两个数字。重复该操作，直到左边已归位的数字比取出的数字更小，或者取 出的数字已经被移到整个序列的最左边为止。

4.由于 5 > 3，所以交换这两个数字。

5.对数字 3 的操作到此结束。此时 3 和 5 已归位，还剩下右边 7 个数字尚未排序。

6.接下来是第 3 轮。和前面一样，取出未排序区域中最左边的数字 4，将它与左边的数字 5 进行比较。

7.由于 5>4，所以交换这两个数字。交换后再把 4 和左边的 3 进行比较，发现 3<4，因为出现了比自己 小的数字，所以操作结束。

8.于是 4 也归位了。此时 3、4、5 都已归位，已排序区域也得到了扩大。

9.遇到左边的数字都比自己小的情况时......

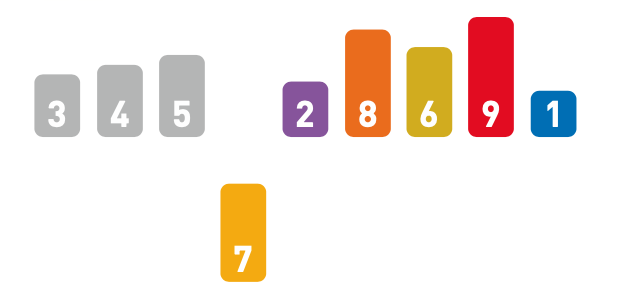
10.不需要任何操作即可完成排序

11.重复上述操作，直到所有数字都归位

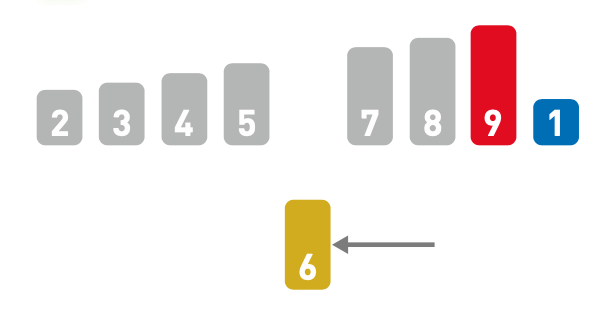
12.对所有数字的操作都结束时，排序也就完成了。

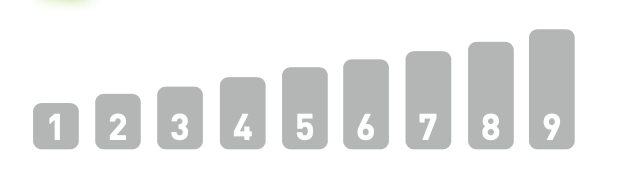
代码实现

func insertionSort(_ arr:[Int]) -> [Int] {
    var ret = arr
    for x in 1..<ret.count {
        var y = x
        let tmp = ret[y]
        while y > 0 && tmp < ret[y - 1] {
            ret[y] = ret[y-1]
            y -= 1
        }
        ret[y] = tmp
    }
    return ret
}

let arr = [5,8,4,7,9,1,6]
let ret = insertionSort(arr)

性能

在插入排序中，需要将取出的数据与其左边的数字进行比较。就跟前面讲的步骤一 样，如果左边的数字更小，就不需要继续比较，本轮操作到此结束，自然也不需要交换 数字的位置。

然而，如果取出的数字比左边已归位的数字都要小，就必须不停地比较大小，交换 数字，直到它到达整个序列的最左边为止。具体来说，就是第 k 轮需要比较 k - 1 次。因 此，在最糟糕的情况下，第 2 轮需要操作 1 次，第 3 轮操作 2 次......第 n 轮操作 n -1 次，所以时间复杂度和冒泡排序的一样，都为 O(n^2)。

输入数据按从大到小的顺序排列时就是最糟糕的情况。