堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为 O(nlogn)，它也是不稳定排序。

堆

二叉堆本质上是一种完全二叉树，它分为两个类型

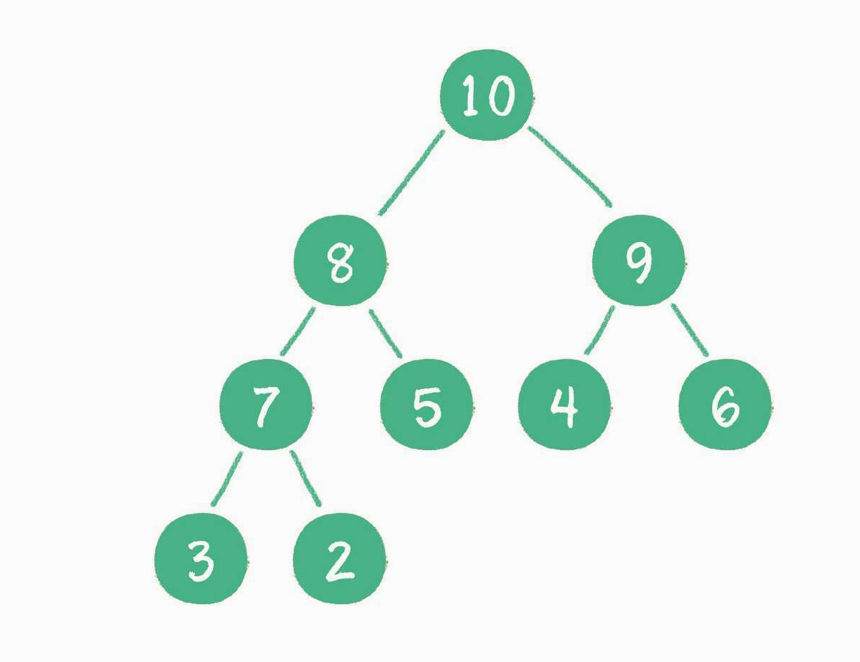
1. 大顶堆：每个结点的值都大于或等于其左右孩子结点的值

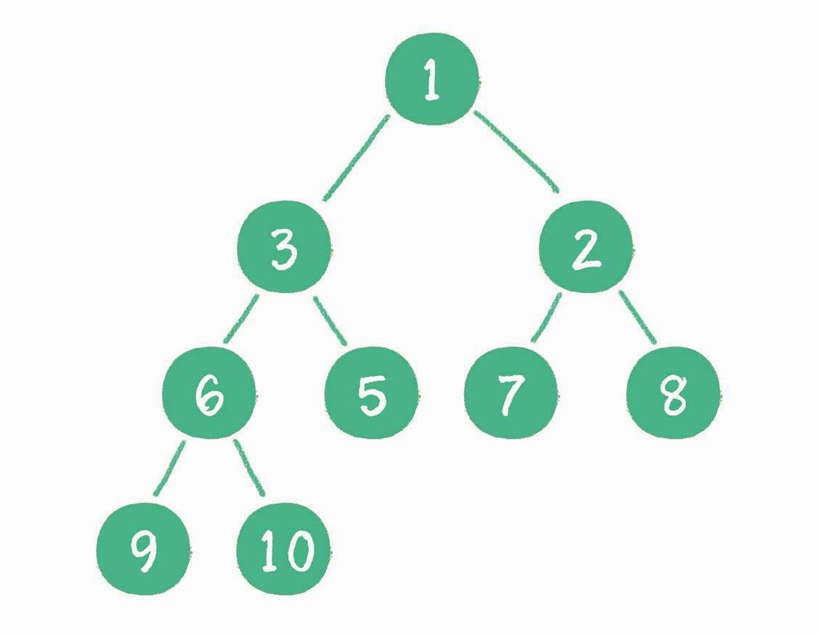
2. 小顶堆：每个结点的值都小于或等于其左右孩子结点的值

二叉堆虽然是一个完全二叉树，但它的存储方式并不是链式存储，而是顺序存储；二叉堆的所有节点都存储在数组中。

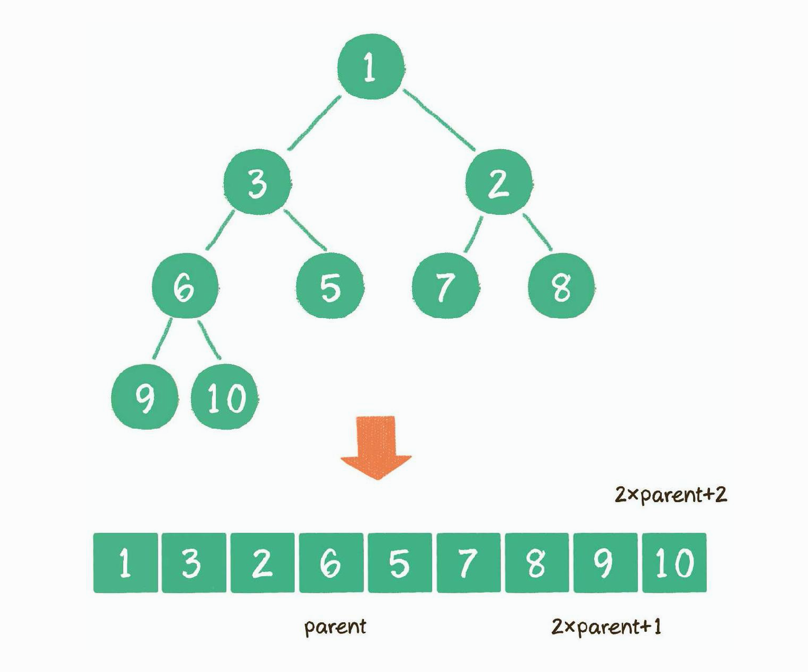
• 大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
• 小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

自我调整

插入节点

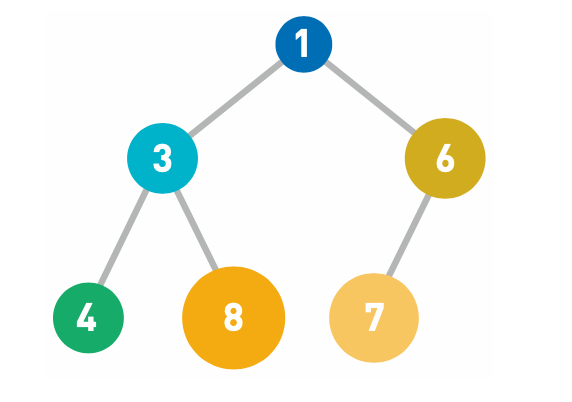
1.往堆里添加数字 5。在堆中存储数据时必须遵守这样一条规则: 子结点必定大于父结点。因此，最小值被存储在顶端的根结点中。往堆中添加数据时，为了遵守这条规则，一般会把新数据放在最下面一行靠左的位置。当最下面一行里没有多余空间时，就再往下另起一行， 把数据加在这一行的最左端。

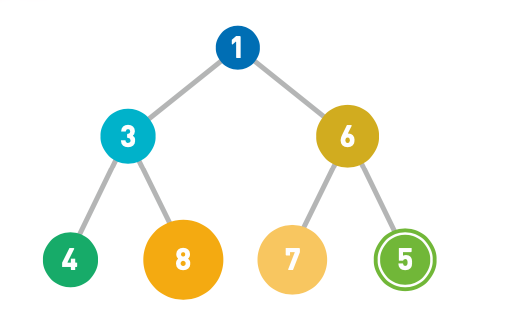
2.如果父结点大于子结点， 则小顶堆的规则，因此需要交换父子结点的位置

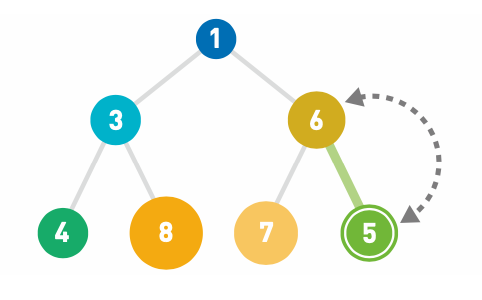
3.这里由于父结点的 6 大于子结点的 5，所以交 换了这两个数字。重复这样的操作直到数据都 符合规则，不再需要交换为止。

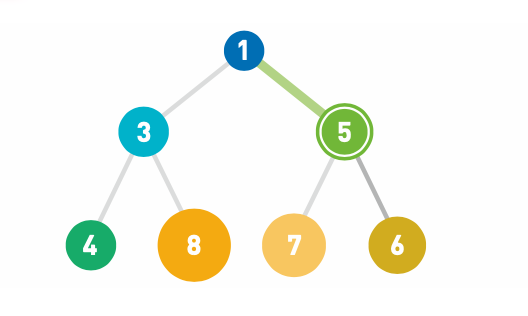
现在，父结点的 1 小于子结点的 5，父结点的数字更小，所以不再交换。

删除节点

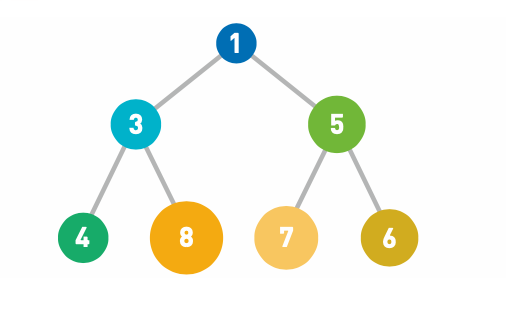
将 1 从堆中移除

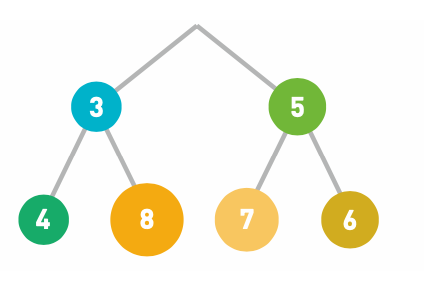
由于最上面的数据被取出，因此堆的结构也需 要重新调整。将最后的数据(此 处为 6)移动到最顶端。

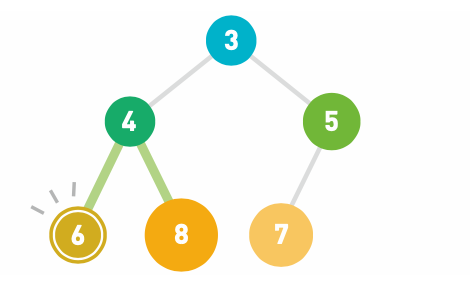
如果子结点的数字小于父结点的，就将父结点 与其左右两个子结点中较小的一个进行交换

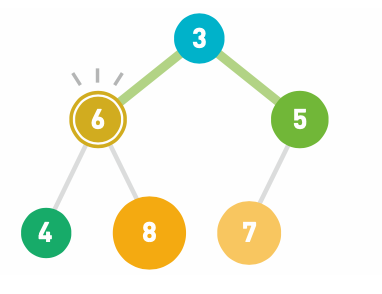
重复操作直到数据都符合规则，不再需要交换为止。

构建二叉堆

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质就是让所有非叶子节点依次“下沉”

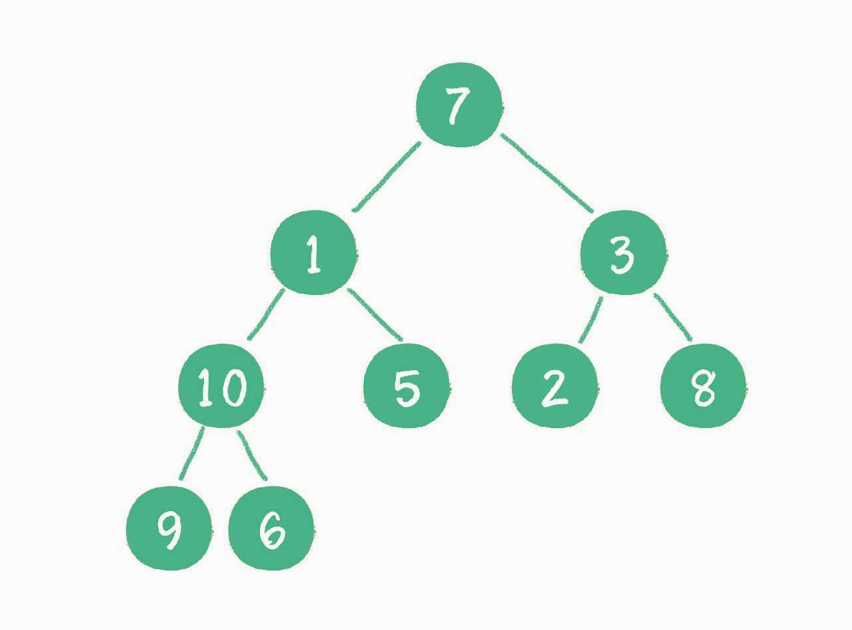
从最后一个非叶子节点开始，也就是从节点 10 开始。如果节点 10 大于它左、右孩子节点中最小的一个，则节点 10“下沉”。

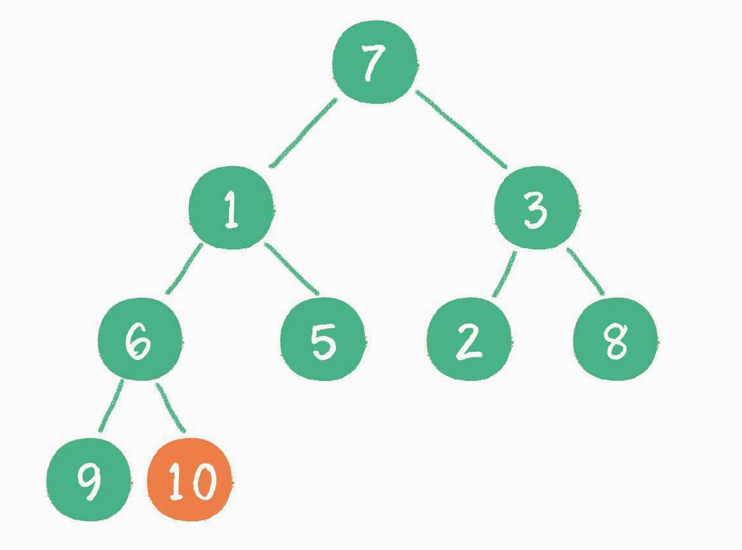
接下来轮到节点 3，如果节点 3 大于它左、右孩子节点中最小的一个，则节点 3“下沉”。

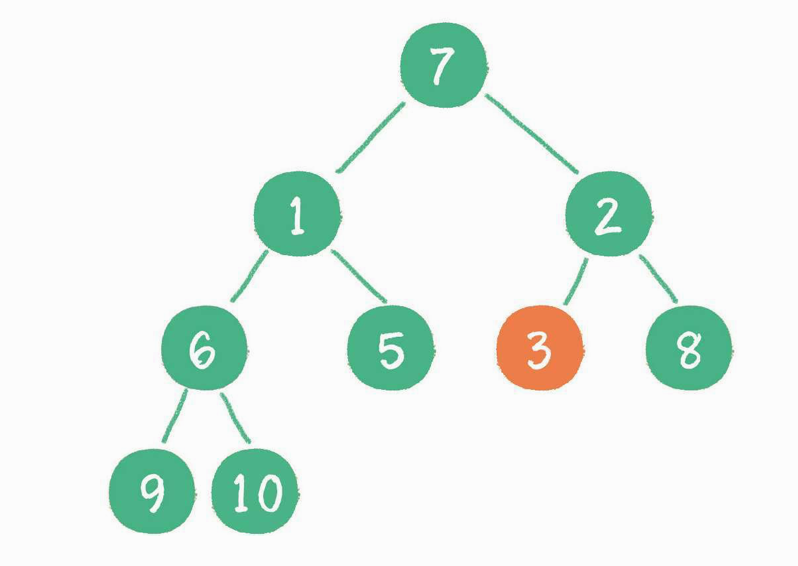
然后轮到节点 1，如果节点 1 大于它左、右孩子节点中最小的一个，则节点 1“下沉”。事实上节点 1 小于它的左、右孩子，所以不用改变。

接下来轮到节点 7，如果节点 7 大于它左、右孩子节点中最小的一个，则节点 7“下沉”。

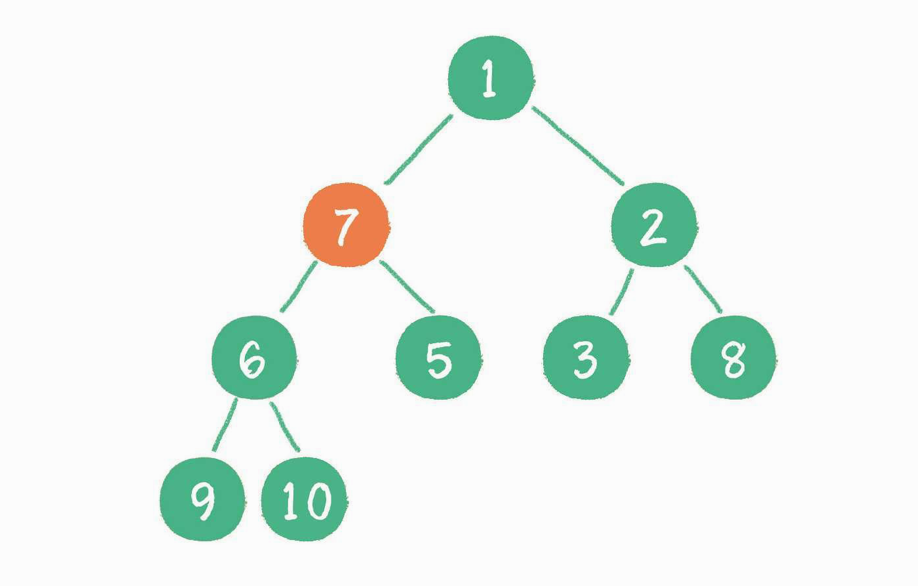
节点 7 继续比较，继续“下沉“

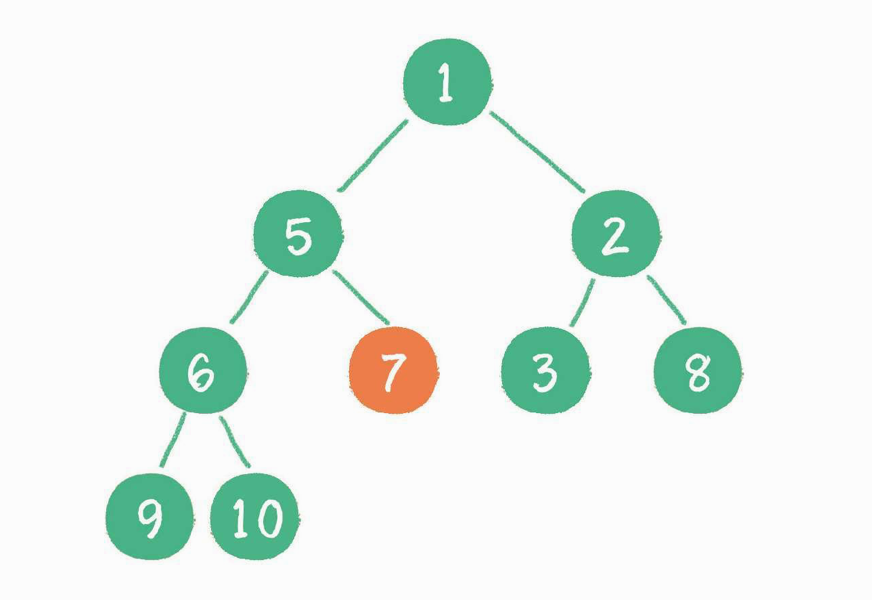
经过上述几轮比较和“下沉”操作，最终每一节点都小于它的左、右孩子节点，一个无序的完全二叉树就被构建成了一个最小堆。

思想

将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余 n-1 个元素重新构造成一个堆，这样会得到 n 个元素的次小值。如此反复执行，便能得到一个有序序列了

代码

构建 Heap 结构

struct Heap<T> {
    var nodes = [T]()

    private var order: (T, T) -> Bool

    init(order: @escaping (T, T) -> Bool) {
        self.order = order
    }

    init(array: [T], order: @escaping (T, T) -> Bool) {
        self.order = order
        configureHeap(from: array)
    }

    private mutating func configureHeap(from array: [T]) {
        nodes = array

        /// 从最后一个非叶子节点开始，依次做“下沉”调整， (n/2 - 1) 或者 (n/2 - 3/2) , 向下取整，所以都是 n/2 - 1
        for i in stride(from: nodes.count/2 - 1, to: 0, by: -1) {
            shiftDown(i)
        }
    }

    var isEmpty: Bool {
        return nodes.isEmpty
    }

    var count: Int {
        return nodes.count
    }

    @inline(__always) internal func parentIndex(ofIndex i: Int) -> Int {
        return (i - 1) / 2
    }

    @inline(__always) internal func leftChildIndex(ofIndex i: Int) -> Int {
        return 2 * i + 1
    }

    @inline(__always) internal func rightChildIndex(ofIndex i: Int) -> Int {
        return 2 * i + 2
    }

    func peek() -> T? {
        return nodes.first
    }

    mutating func insert(_ value: T) {
        nodes.append(value)
        shiftUp(nodes.count - 1)
    }

    mutating func replace(index i: Int, value: T) {
        guard i < nodes.count else {
            return
        }
        remove(at: i)
        insert(value)
    }

    mutating func remove(at index: Int) -> T? {
        guard index < nodes.count else { return nil }

        let size = nodes.count - 1
        if index != size {
          nodes.swapAt(index, size)
          shiftDown(from: index, until: size)
          shiftUp(index)
        }
        return nodes.removeLast()
    }

    mutating func shiftUp(_ index: Int) {

        var childIndex = index
        let child = nodes[childIndex]

        var parentIndex = self.parentIndex(ofIndex: childIndex)

        while childIndex > 0 && order(child, nodes[parentIndex]) {
          nodes[childIndex] = nodes[parentIndex]
          childIndex = parentIndex
          parentIndex = self.parentIndex(ofIndex: childIndex)
        }
        nodes[childIndex] = child
    }

    mutating func shiftDown(from index: Int, until endIndex: Int) {
        let leftChildIndex = self.leftChildIndex(ofIndex: index)
        let rightChildIndex = leftChildIndex + 1

        var first = index

        /// 左节点
        if leftChildIndex < endIndex && order(nodes[leftChildIndex], nodes[first]) {
            first = leftChildIndex
        }

        /// 右节点
        if rightChildIndex < endIndex && order(nodes[rightChildIndex], nodes[first]) {
            first = rightChildIndex
        }

        if first == index { return }

        /// 调整
        nodes.swapAt(index, first)

        shiftDown(from: first, until: endIndex)
    }

    mutating func shiftDown(_ index: Int) {
        shiftDown(from: index, until: nodes.count)
    }
}

以下是在 Swift 中实现堆排序的方法：

extension Heap {
  public mutating func sort() -> [T] {
    for i in stride(from: (elements.count - 1), through: 1, by: -1) {
      swap(&elements[0], &elements[i])
      shiftDown(0, heapSize: i)
    }
    return elements
  }
}

为堆实现添加了一个sort()函数。 这个函数的使用方式：

var h1 = Heap(array: [5, 13, 2, 25, 7, 17, 20, 8, 4], sort: >)
let a1 = h1.sort()

因为我们需要一个max-heap来从低到高排序，你需要给Heap提供 sort 函数的反向排序。 要对<进行排序，必须使用>作为 sort 函数创建Heap对象。 换句话说，从低到高的排序会创建一个 max-heap 并将其转换为 min-heap（ 译注： 这边的意思就是排完序以后就变成了一个从小到大的特殊的 min-heap）。

我们可以为此编写一个方便的辅助函数：

public func heapsort<T>(_ a: [T], _ sort: @escaping (T, T) -> Bool) -> [T] {
  let reverseOrder = { i1, i2 in sort(i2, i1) }
  var h = Heap(array: a, sort: reverseOrder)
  return h.sort()
}

使用方式：

let a2 = heapsort([5, 13, 2, 25, 7, 17, 20, 8, 4], <)
print(a2)