希尔排序
# 介绍
希尔排序是插入排序的一种又称“缩小增量排序”,是直接插入排序算法的一种更高效的改进版本,希尔排序是非稳定排序算法,该方法因“D.L.Shell”于 1959 年提出而得名。
插入排序在小规模数据或者基本有序时非常高效,数据有序程度越高,越高效。而希尔排序就是对它的一种改良,使得它对较大规模并且无序的数据也非常有效率。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位;
# 思路
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止。
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
# 图解
1.排序下面序列(原始数组,元素颜色相同的为一组)

2.初始增量 gap = length / 2 = 5,也就是说整个数组分成 5 组:[8, 3] [9, 5] [1, 4] [7, 6] [2, 0]
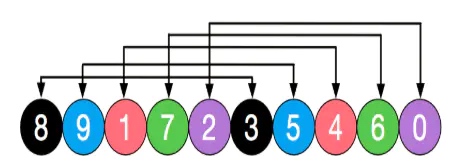
3.对这 5 组进行插入排序,结果如下,之后缩小增量 gap = 5 / 2 = 2,数组分成了 2 组:[3, 1, 0, 9, 7] [5, 6, 8, 4, 2]
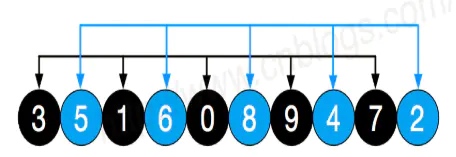
4.再对上面两个数组进行插入排序,结果如下,再次缩小增量 gap = 2 / 2 = 1,整个数组只有一组数据了[0, 2, 1, 4, 3, 5, 7, 6, 9, 8]
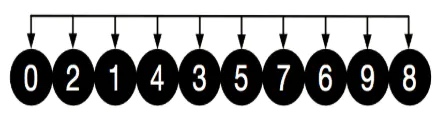
5.之后只需对这个数组进行微调,无需进行大量的移动操作,即可完成整个数组的排序

# 代码实现
var tmp = [4,32,5,6,8,10,31,7]
/// 希尔排序
func insertSort(_ list: inout[Int], start: Int, gap: Int) {
for i in stride(from: (start + gap), to: list.count, by: gap) {
let currentValue = list[i]
var pos = i
while pos > gap && list[pos - gap] > currentValue {
list[pos] = list[pos - gap]
pos -= gap
}
list[pos] = currentValue
}
}
func shellSort(_ list: inout [Int]) {
var sublistCount = list.count / 2
while sublistCount > 0 {
for pos in 0..<sublistCount {
insertSort(&list, start: pos, gap: sublistCount)
}
sublistCount = sublistCount / 2
}
}
shellSort(&tmp)
# 性能
在大多数情况下,希尔排序的性能为 O(n^2),如果幸运,则为 O(nlogn)。 该算法是不稳定的排序,它可能会改变具有相等值的元素的相对顺序。
步长的选择是希尔排序的重要部分。只要最终步长为 1 任何步长序列都可以工作。算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序,最终算法以步长为 1 进行排序。当步长为 1 时,算法变为普通插入排序,这就保证了数据一定会被排序。
